如图1，矩形 的顶点 ， 的坐标分别为 ， ，直线 交 于点 ， ，抛物线 过 ， 两点．
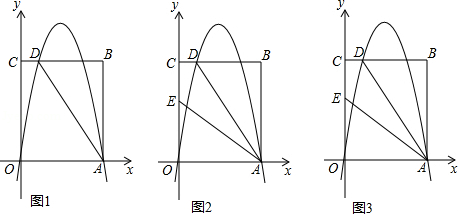
（1）求点 的坐标和抛物线 的表达式；
（2）点 是抛物线 对称轴上一动点，当 时，求所有符合条件的点 的坐标；
（3）如图2，点 ，连接 ，将抛物线 的图象向下平移 个单位得到抛物线 ．
①设点 平移后的对应点为点 ，当点 恰好在直线 上时，求 的值；
②当 时，若抛物线 与直线 有两个交点，求 的取值范围．
某校为了解初三年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：kg）分成五组
（A:39．5~46．5;B:46．5~53．5;C:53．5~60．5;D:60．5~67．5;E:67．5~74．5），并依据统计数据绘制了如下两个不完整的统计图．
解答下列问题：
（1）这次抽样调查的样本容量是，并不全频数分布直方图；
（2）C组学生的频率为，在扇形统计图中D组的圆心角是度；
（3）请你估计该校初三年级体重超过60kg的学生大约有多少名？
；
已知：一次函数
的图象与反比例函数
（
）的图象相交于A，B两点（A在B的右侧）．
（1）当A（4，2）时，求反比例函数的解析式及B点的坐标；
（2）在（1）的条件下，反比例函数图象的另一支上是否存在一点P，使△PAB是以AB为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
（3）当A（a，﹣2a+10），B（b，﹣2b+10）时，直线OA与此反比例函数图象的另一支交于另一点C，连接BC交y轴于点D．若
，求△ABC的面积．
如图，在矩形ABCD中，AB=5，AD=3，点P是AB边上一点（不与A，B重合），连接CP，过点P作PQ⊥CP交AD边于点Q，连接CQ．
（1）当△CDQ≌△CPQ时，求AQ的长；
（2）取CQ的中点M，连接MD，MP，若MD⊥MP，求AQ的长．
粤公网安备 44130202000953号