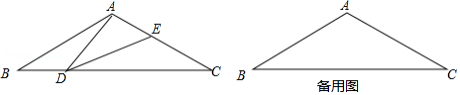
如图,在等腰三角形 中, , ,点 是 边上的一个动点(不与 、 重合),在 上取一点 ,使 .
(1)求证: ;
(2)设 , ,求 关于 的函数关系式并写出自变量 的取值范围;
(3)当 是等腰三角形时,求 的长.
相关知识点
推荐套卷
如图,在等腰三角形 中, , ,点 是 边上的一个动点(不与 、 重合),在 上取一点 ,使 .
(1)求证: ;
(2)设 , ,求 关于 的函数关系式并写出自变量 的取值范围;
(3)当 是等腰三角形时,求 的长.
