作图题:有公路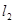 同侧、
同侧、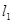 异侧的两个城镇A、B,如下图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路
异侧的两个城镇A、B,如下图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路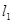 、
、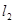 的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置。(保留作图痕迹,不写作法).
的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置。(保留作图痕迹,不写作法).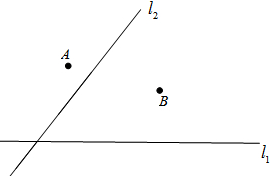
作图题:有公路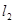 同侧、
同侧、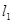 异侧的两个城镇A、B,如下图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路
异侧的两个城镇A、B,如下图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路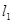 、
、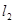 的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置。(保留作图痕迹,不写作法).
的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置。(保留作图痕迹,不写作法).