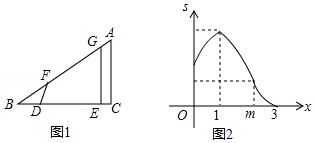
如图1, 中, ,线段 在射线 上,且 ,线段 沿射线 运动,开始时,点 与点 重合,点 到达点 时运动停止,过点 作 ,与射线 相交于点 ,过点 作 的垂线,与射线 相交于点 .设 ,四边形 与 重叠部分的面积为 , 关于 的函数图象如图2所示(其中 , , 时,函数的解析式不同)
(1)填空: 的长是 ;
(2)求 关于 的函数关系式,并写出 的取值范围.
相关知识点
推荐套卷
如图1, 中, ,线段 在射线 上,且 ,线段 沿射线 运动,开始时,点 与点 重合,点 到达点 时运动停止,过点 作 ,与射线 相交于点 ,过点 作 的垂线,与射线 相交于点 .设 ,四边形 与 重叠部分的面积为 , 关于 的函数图象如图2所示(其中 , , 时,函数的解析式不同)
(1)填空: 的长是 ;
(2)求 关于 的函数关系式,并写出 的取值范围.
