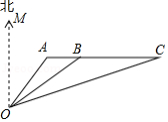
如图,码头 、 分别在海岛 的北偏东 和北偏东 方向上,仓库 在海岛 的北偏东 方向上,码头 、 均在仓库 的正西方向,码头 和仓库 的距离 ,若将一批物资从仓库 用汽车运送到 、 两个码头中的一处,再用货船运送到海岛 ,若汽车的行驶速度为 ,货船航行的速度为 ,问这批物资在哪个码头装船,最早运抵海岛 ?(两个码头物资装船所用的时间相同,参考数据: ,
相关知识点
推荐套卷
如图,码头 、 分别在海岛 的北偏东 和北偏东 方向上,仓库 在海岛 的北偏东 方向上,码头 、 均在仓库 的正西方向,码头 和仓库 的距离 ,若将一批物资从仓库 用汽车运送到 、 两个码头中的一处,再用货船运送到海岛 ,若汽车的行驶速度为 ,货船航行的速度为 ,问这批物资在哪个码头装船,最早运抵海岛 ?(两个码头物资装船所用的时间相同,参考数据: ,
