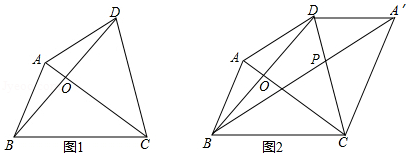
如图1,四边形 的对角线 , 相交于点 , , , , , .
(1)填空: 与 的数量关系为 ;
(2)求 的值;
(3)将 沿 翻折,得到△ (如图 ,连接 ,与 相交于点 .若 ,求 的长.
相关知识点
推荐套卷
如图1,四边形 的对角线 , 相交于点 , , , , , .
(1)填空: 与 的数量关系为 ;
(2)求 的值;
(3)将 沿 翻折,得到△ (如图 ,连接 ,与 相交于点 .若 ,求 的长.
