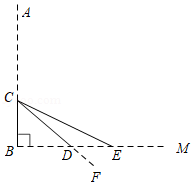
如图,池塘边一棵垂直于水面 的笔直大树 在点 处折断, 部分倒下,点 与水面上的点 重合,部分沉入水中后,点 与水中的点 重合, 交水面于点 , , , ,求 部分的高度.(精确到 .参考数据: ,
相关知识点
推荐套卷
如图,池塘边一棵垂直于水面 的笔直大树 在点 处折断, 部分倒下,点 与水面上的点 重合,部分沉入水中后,点 与水中的点 重合, 交水面于点 , , , ,求 部分的高度.(精确到 .参考数据: ,
