鹏鹏童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反应:每降价1元,每星期可多卖10件.已知该款童装每件成本30元.设该款童装每件售价 元,每星期的销售量为 件.
(1)求 与 之间的函数关系式(不求自变量的取值范围);
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)①当每件童装售价定为多少元时,该店一星期可获得3910元的利润?
②若该店每星期想要获得不低于3910元的利润,则每星期至少要销售该款童装多少件?
相关知识点
推荐套卷
 ).
).

 .
.
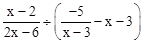 ,其中
,其中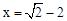 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号