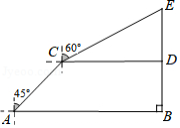
为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理.如图,我国一艘海监船在 处巡航时,监测到在正东方向的 处有一艘可疑船只正匀速向正北方向航行,我国海监船立即沿北偏东 方向对该船只实施拦截,航行 后到达 处,发现此时可疑船只在正东方向的 处,我国海监船决定改变航向,沿北偏东 方向继续加速航行,又航行 后在 处将该可疑船只成功拦截(结果保留根号)
(1)求当我国海监船到达 处时,离可疑船只的距离 ;
(2)成功拦截后,发现整个过程用时 ,求可疑船只的航行速度.
相关知识点
推荐套卷
 ,其中x = -2,y =
,其中x = -2,y =  .
. .(2)
.(2)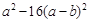 .
. ∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;
∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;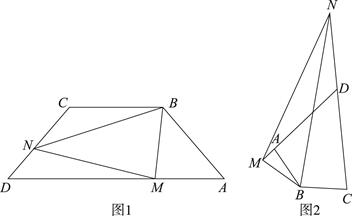
 粤公网安备 44130202000953号
粤公网安备 44130202000953号