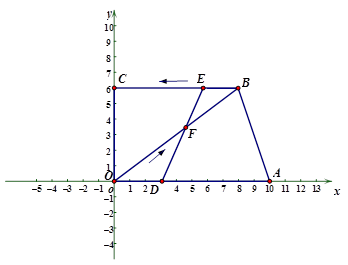
如图,在平面直角坐标系中,点A(10,0),点C(0,6),,BC∥OA,OB=10,点E从点B出发,以每秒1个单位长度沿BC向点C运动,点F从点O出发,以每秒2个单位长度沿OB向点B运动,现点E、F同时出发,连接EF并延长交OA于点D,当F点到达B点时,E、F两点同时停止运动。设运动时间为t秒当四边形OCED是矩形时,求t的值;
当△BEF的面积最大时,求t的值;
当以BE为直径的圆经过点F时,求t的值;
当动点E、F会同时在某个反比例函数的图像上时,求t的值.(直接写出答案)
相关知识点
推荐套卷
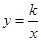 (k为常数,
(k为常数,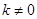 )图象上的“理想点”,求这个反比例函数的表达式;
)图象上的“理想点”,求这个反比例函数的表达式;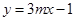 (m为常数,
(m为常数,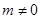 )的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.
)的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.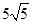 ,且
,且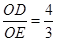 ,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:
,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l: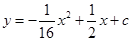 经过点E,且与AB边相交于点F.
经过点E,且与AB边相交于点F.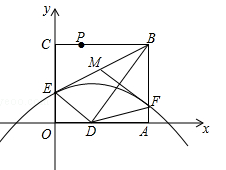
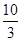 ),连接MN.
),连接MN.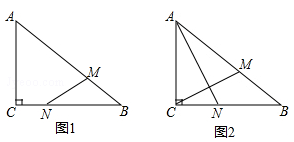
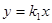 和
和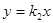 与反比例函数
与反比例函数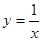 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.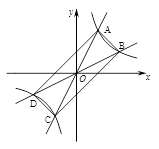
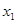 ,
,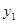 ),Q(
),Q(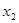 ,
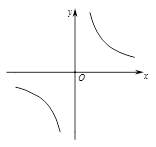
,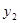 )(x2 > x1 > 0)是函数
)(x2 > x1 > 0)是函数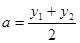 ,
,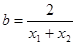 ,试判断
,试判断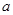 ,
,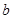 的大小关系,并说明理由.
的大小关系,并说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号