菱形 中、 ,点 为射线 上的动点,作射线 与直线 相交于点 ,将射线 绕点 逆时针旋转 ,得到射线 ,射线 与直线 相交于点 .
(1)如图①,点 与点 重合时,点 , 分别在线段 , 上,请直接写出 , , 三条段段之间的数量关系;
(2)如图②,点 在 的延长线上,且 , , 分别在线段 的延长线和线段 的延长线上,请写出 , , 三条线段之间的数量关系,并说明理由;
(3)点 在线段 上,若 , ,当 时,请直接写出 的长.

相关知识点
推荐套卷
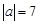 ,
,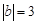 ,a,b同号。求a+b的值 (本题6分)
,a,b同号。求a+b的值 (本题6分)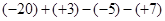
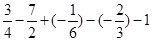
 ,
, ,
, ,
,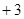 ,
,
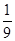 ,-5,
,-5,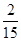 ,0,-5.3,
,0,-5.3,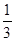 。
。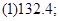 (2)
(2)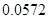 ;(3)
;(3)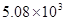
 粤公网安备 44130202000953号
粤公网安备 44130202000953号