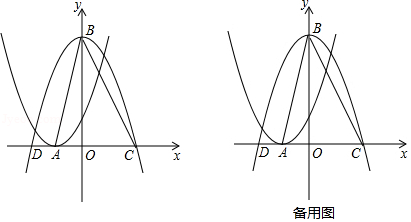
如图所示,将二次函数 的图象沿 轴翻折,然后向右平移1个单位,再向上平移4个单位,得到二次函数 的图象.函数 的图象的顶点为点 .函数 的图象的顶点为点 ,和 轴的交点为点 , (点 位于点 的左侧).
(1)求函数 的解析式;
(2)从点 , , 三个点中任取两个点和点 构造三角形,求构造的三角形是等腰三角形的概率;
(3)若点 是线段 上的动点,点 是 三边上的动点,是否存在以 为斜边的 ,使 的面积为 面积的 ?若存在,求 的值;若不存在,请说明理由.
相关知识点
推荐套卷
 粤公网安备 44130202000953号
粤公网安备 44130202000953号