如图,平面直角坐标系内,小正方形网格的边长为1个单位长度, 的三个顶点的坐标分别为 , , .
(1)画出 关于 轴的对称图形△ ;
(2)画出将 绕原点 逆时针方向旋转 得到的△ ;
(3)求(2)中线段 扫过的图形面积.
推荐套卷
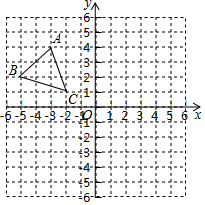
如图,平面直角坐标系内,小正方形网格的边长为1个单位长度, 的三个顶点的坐标分别为 , , .
(1)画出 关于 轴的对称图形△ ;
(2)画出将 绕原点 逆时针方向旋转 得到的△ ;
(3)求(2)中线段 扫过的图形面积.
