天水市“最美女教师”刘英为抢救两名学生，身负重伤．社会各界纷纷为她捐款，某校2000名学生也积极参加了此捐款活动．捐款金额有5元、10元、15元、20元、25元共五种．为了了解捐款情况，学校随机抽样调查了部分学生的捐款情况，并根据捐款金额和人数绘制了如下统计图（图①和图② ．请根据所给信息解答下列问题．
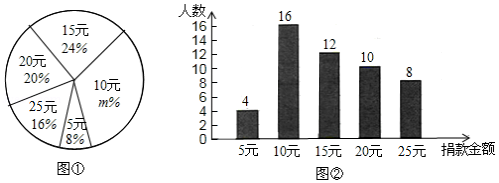
（1）本次接受随机抽样调查的学生人数为 人，图①中 的值是 ．
（2）根据样本数据，请估计该校在本次活动中捐款金额为10元的学生人数．
相关试题
某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售2辆A型车和1辆B型车，销售额为62万元．
（1）求每辆A型车和B型车的售价各多少万元．
（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元．则有哪几种购车方案?
已知：如图，在
中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．
（1）求证：△DOE≌△BOF．
（2）当∠DOE等于多少度时，四边形BFDE为菱形?请说明理由．
某校为了了解学生孝敬父母的情况（选项：A为父母洗一次脚；B帮父母做一次家务；C给父母买一件礼物；D其它），在全校范围内随机抽取了若干名学生进行调查，得到如下图表（部分信息未给出）：
根据以上信息解答下列问题：
（1）这次被调查的学生有多少人?
（2）求表中m，n，p的值，并补全条形统计图．
（3）该校有1600名学生，估计该校全体学生中选择B选项的有多少人?
．
；
．推荐套卷
粤公网安备 44130202000953号