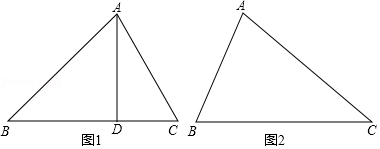
已知:如图1,在锐角 中, , , , 于 .
在 中, ,则 ;
在 中, ,则 ;
所以, ,即, ,
进一步即得正弦定理: (此定理适合任意锐角三角形).
参照利用正弦定理解答下题:
如图2,在 中, , , ,求 的长.
相关知识点
推荐套卷
已知:如图1,在锐角 中, , , , 于 .
在 中, ,则 ;
在 中, ,则 ;
所以, ,即, ,
进一步即得正弦定理: (此定理适合任意锐角三角形).
参照利用正弦定理解答下题:
如图2,在 中, , , ,求 的长.
