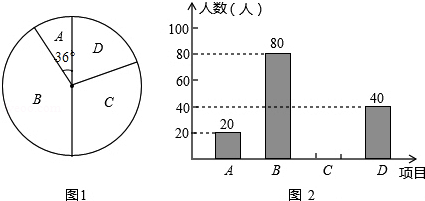
某学校为了增强学生体质，决定开设以下体育课外活动项目： 篮球、 乒乓球、 跳绳、 踢毽子，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：
（1）这次被调查的学生共有 人；
（2）请你将条形统计图补充完成；
（3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．
=
=－
；（2）
=
；（4）
；（5）
；（6）
；
；
)×(－1
)÷(－2
)；推荐套卷
某学校为了增强学生体质，决定开设以下体育课外活动项目： 篮球、 乒乓球、 跳绳、 踢毽子，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：
（1）这次被调查的学生共有 人；
（2）请你将条形统计图补充完成；
（3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．
粤公网安备 44130202000953号