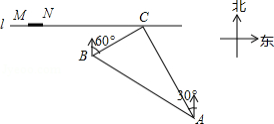
如图，在一条笔直的东西向海岸线 上有一长为 的码头 和灯塔 ，灯塔 距码头的东端 有 ．一轮船以 的速度航行，上午 在 处测得灯塔 位于轮船的北偏西 方向，上午 在 处测得灯塔 位于轮船的北偏东 方向，且与灯塔 相距 ．
（1）若轮船照此速度与航向航行，何时到达海岸线？
（2）若轮船不改变航向，该轮船能否停靠在码头？请说明理由．（参考数据： ，
在实数范围内成立，其中
，
，
是两两不同的实数，求
。
∠CAB．
，求BC和BF的长．
其中
．
，其中
。相关知识点
推荐套卷
如图，在一条笔直的东西向海岸线 上有一长为 的码头 和灯塔 ，灯塔 距码头的东端 有 ．一轮船以 的速度航行，上午 在 处测得灯塔 位于轮船的北偏西 方向，上午 在 处测得灯塔 位于轮船的北偏东 方向，且与灯塔 相距 ．
（1）若轮船照此速度与航向航行，何时到达海岸线？
（2）若轮船不改变航向，该轮船能否停靠在码头？请说明理由．（参考数据： ，
粤公网安备 44130202000953号