下面是某年参加国家教育评估的学校学生的数学平均成绩(x)的统计图,请根据所给信息,解答下列问题:
(1)本次共调查 所学校.
(2) 图能更好地说明一半以上学校的学生数学平均成绩在 之间.
(3)估计我国150所学校中学生的数学平均成绩在 的学校有多少所?
推荐套卷
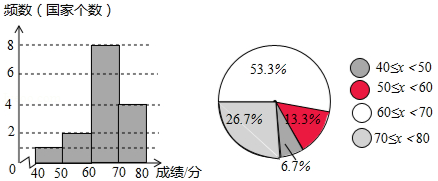
下面是某年参加国家教育评估的学校学生的数学平均成绩(x)的统计图,请根据所给信息,解答下列问题:
(1)本次共调查 所学校.
(2) 图能更好地说明一半以上学校的学生数学平均成绩在 之间.
(3)估计我国150所学校中学生的数学平均成绩在 的学校有多少所?
