早晨,小明步行到离家900米的学校去上学,到学校时发现眼镜忘在家中,于是他立即按原路步行回家,拿到眼镜后立即按原路骑自行车返回学校.已知小明步行从学校到家所用的时间比他骑自行车从家到学校所用的时间多10分钟,小明骑自行车速度是步行速度的3倍.
(1)求小明步行速度(单位:米/分)是多少;
(2)下午放学后,小明骑自行车回到家,然后步行去图书馆,如果小明骑自行车和步行的速度不变,小明步行从家到图书馆的时间不超过骑自行车从学校到家时间的2倍,那么小明家与图书馆之间的路程最多是多少米?
相关知识点
推荐套卷
 +
+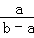 )÷
)÷ ,其中a,b满足
,其中a,b满足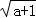 +|b﹣
+|b﹣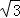 |=0.
|=0. 是方程
是方程 的一个实数根,则代数式
的一个实数根,则代数式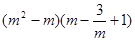 的值为.
的值为.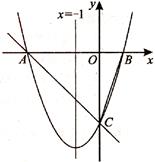
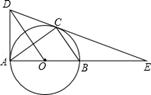
 ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π) 粤公网安备 44130202000953号
粤公网安备 44130202000953号