襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为: .
(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
相关知识点
推荐套卷

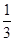 BE,AB=16cm,求BE的长.
BE,AB=16cm,求BE的长. 图所示,是正方体展开图的各面编号,指出相对两面的号码组合(相对面没有公共棱),再指出与面6相邻的面.
图所示,是正方体展开图的各面编号,指出相对两面的号码组合(相对面没有公共棱),再指出与面6相邻的面.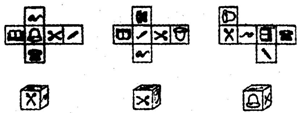
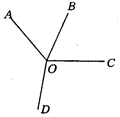
 ON的度数(结果用含β的式子表示).
ON的度数(结果用含β的式子表示).
 粤公网安备 44130202000953号
粤公网安备 44130202000953号