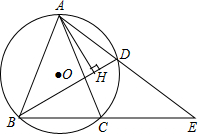
如图,△ ABC内接于⊙ O, BC=2, AB= AC,点 D为 上的动点,且cos∠ ABC= .
(1)求 AB的长度;
(2)在点 D的运动过程中,弦 AD的延长线交 BC延长线于点 E,问 AD• AE的值是否变化?若不变,请求出 AD• AE的值;若变化,请说明理由;
(3)在点 D的运动过程中,过 A点作 AH⊥ BD,求证: BH= CD+ DH.
推荐套卷
如图,△ ABC内接于⊙ O, BC=2, AB= AC,点 D为 上的动点,且cos∠ ABC= .
(1)求 AB的长度;
(2)在点 D的运动过程中,弦 AD的延长线交 BC延长线于点 E,问 AD• AE的值是否变化?若不变,请求出 AD• AE的值;若变化,请说明理由;
(3)在点 D的运动过程中,过 A点作 AH⊥ BD,求证: BH= CD+ DH.
