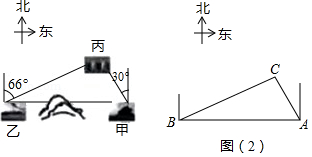
如图，已知甲地在乙地的正东方向，因有大山阻隔，由甲地到乙地需要绕行丙地．已知丙地位于甲地北偏西30°方向，距离甲地460 km，丙地位于乙地北偏东66°方向，现要打通穿山隧道，建成甲乙两地直达高速公路，如果将甲、乙、丙三地当作三个点 A、 B、 C，可抽象成图（2）所示的三角形，求甲乙两地之间直达高速线路的长 AB（结果用含非特殊角的三角函数和根式表示即可）．
相关试题
BE，AB=16cm，求BE的长．
图所示，是正方体展开图的各面编号，指出相对两面的号码组合（相对面没有公共棱），再指出与面6相邻的面．
ON的度数(结果用含β的式子表示).
相关知识点
推荐套卷
如图，已知甲地在乙地的正东方向，因有大山阻隔，由甲地到乙地需要绕行丙地．已知丙地位于甲地北偏西30°方向，距离甲地460 km，丙地位于乙地北偏东66°方向，现要打通穿山隧道，建成甲乙两地直达高速公路，如果将甲、乙、丙三地当作三个点 A、 B、 C，可抽象成图（2）所示的三角形，求甲乙两地之间直达高速线路的长 AB（结果用含非特殊角的三角函数和根式表示即可）．
粤公网安备 44130202000953号