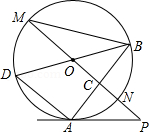
如图, PA为⊙ O的切线, A为切点,直线 PO交⊙ O于点 M、 N,过点 A作 PO的垂线 AB,垂足为 C,交⊙ O于点 B,延长 BO与⊙ O交于点 D,连接 AD、 BM.
(1)等式 OD 2= OC• OP成立吗?若成立,请加以证明;若不成立,请说明理由.
(2)若 AD=6,tan∠ M= ,求sin∠ D的值.
相关知识点
推荐套卷
如图, PA为⊙ O的切线, A为切点,直线 PO交⊙ O于点 M、 N,过点 A作 PO的垂线 AB,垂足为 C,交⊙ O于点 B,延长 BO与⊙ O交于点 D,连接 AD、 BM.
(1)等式 OD 2= OC• OP成立吗?若成立,请加以证明;若不成立,请说明理由.
(2)若 AD=6,tan∠ M= ,求sin∠ D的值.
