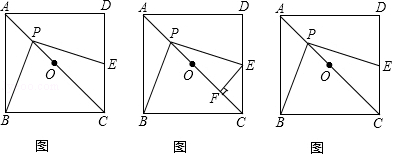
如图①，正方形 ABCD中，点 O是对角线 AC的中点，点 P是线段 AO上（不与 A， O重合）的一个动点，过点 P作 PE⊥ PB且 PE交边 CD于点 E．
（1）求证： PB＝ PE．
（2）如图②，若正方形 ABCD的边长为2，过 E作 EF⊥ AC于点 F，在 P点运动的过程中， PF的长度是否发生变化？若不变，试求出这个不变的值；若变化，请说明理由．
（3）如图③，用等式表示线段 PC， PA， CE之间的数量关系．
相关试题
是⊙
的直径，
是⊙
是切点，
与⊙
.
，
，求
为
是⊙甲、乙、丙、丁四位同学进行一次乒乓球单打比赛，要从中选出两位同学打第一场比赛．
（1）请用树状图法或列表法，求恰好选中甲、丙两位同学的概率；
（2）若已确定甲打第一场，再从其余三位同学中随机选取一位，求恰好选中乙同学的概率．
的图象与y轴交于点A，一次函数
的图象 经过点B（0，－1），并且与x轴以及
相关知识点
推荐套卷
粤公网安备 44130202000953号