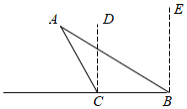
如图,海中有一个小岛 ,它周围10海里内有暗礁,渔船跟踪鱼群由东向西航行,在 点测得小岛 在北偏西 方向上,航行12海里到达 点,这时测得小岛 在北偏西 方向上,如果渔船不改变方向继续向西航行,有没有触礁的危险?并说明理由.(参考数据:
相关知识点
推荐套卷
如图,海中有一个小岛 ,它周围10海里内有暗礁,渔船跟踪鱼群由东向西航行,在 点测得小岛 在北偏西 方向上,航行12海里到达 点,这时测得小岛 在北偏西 方向上,如果渔船不改变方向继续向西航行,有没有触礁的危险?并说明理由.(参考数据:
