某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度 与时间 之间的函数关系,其中线段 、 表示恒温系统开启阶段,双曲线的一部分 表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度 与时间 的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于 时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?

相关知识点
推荐套卷
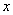 ,
,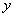 满足
满足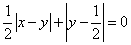 ,求
,求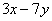 的值.
的值.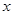 集,甲、乙两部连续剧的收视观众的人次的总和为
集,甲、乙两部连续剧的收视观众的人次的总和为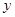 万人次,求
万人次,求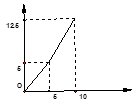
 .等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t.
.等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t. 的长度;
的长度; 平移的过程中,记
平移的过程中,记 相互重叠的面积为
相互重叠的面积为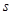 ,请直接写出面积
,请直接写出面积 的函数关系式,并写出
的函数关系式,并写出 与线段
与线段 交于点
交于点 ,连接
,连接 .是否存在这样的时间
.是否存在这样的时间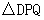 为等腰三角形?若存在,求出对应的
为等腰三角形?若存在,求出对应的

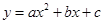 交
交 轴于A、B两点(点A在点B左侧),与
轴于A、B两点(点A在点B左侧),与 轴交于点C,点A、C的坐标分别为(-3,0),(0,3),对称轴直线
轴交于点C,点A、C的坐标分别为(-3,0),(0,3),对称轴直线 交
交 ,,求点P的坐标;
,,求点P的坐标;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号