为了解某校学生对球类运动的喜爱情况，调查小组就打排球、打乒乓球、打篮球、踢足球四项球类运动对该校学生进行了“你最喜爱的球类运动”的抽样调查，并根据调查结果绘制成如图统计图．
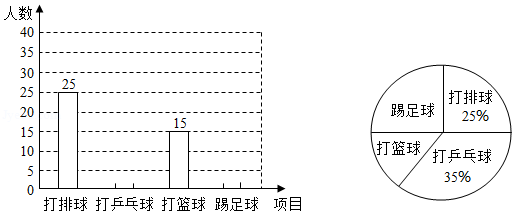
（1）本次抽样调查的样本容量是 ；
（2）补全条形统计图；
（3）该校共有2000名学生，请你估计该校最喜爱“打篮球”的学生人数．
，其中
，
.
在平面直角坐标系中的位置如图
的图象；
关于直线
，并写出
（
，
）是
的坐标为.
、
、
三点在同一条直线上，
，
，
．
推荐套卷
为了解某校学生对球类运动的喜爱情况，调查小组就打排球、打乒乓球、打篮球、踢足球四项球类运动对该校学生进行了“你最喜爱的球类运动”的抽样调查，并根据调查结果绘制成如图统计图．
（1）本次抽样调查的样本容量是 ；
（2）补全条形统计图；
（3）该校共有2000名学生，请你估计该校最喜爱“打篮球”的学生人数．
粤公网安备 44130202000953号