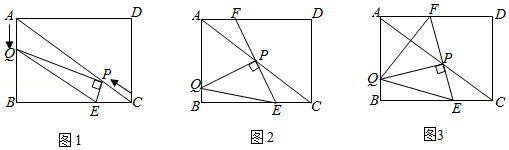
如图1,在矩形 中, , ,动点 , 分别从 点, 点同时以每秒1个单位长度的速度出发,且分别在边 , 上沿 , 的方向运动,当点 运动到点 时, , 两点同时停止运动.设点 运动的时间为 ,连接 ,过点 作 , 与边 相交于点 ,连接 .
(1)如图2,当 时,延长 交边 于点 .求证: ;
(2)在(1)的条件下,试探究线段 , , 三者之间的等量关系,并加以证明;
(3)如图3,当 时,延长 交边 于点 ,连接 ,若 平分 ,求 的值.
相关知识点
推荐套卷

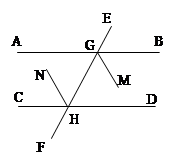
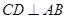 于D,点E为BC边上的任意一点,
于D,点E为BC边上的任意一点,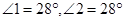
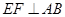 于F,且
于F,且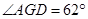 ,求
,求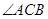 的度数。
的度数。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号