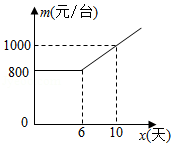
某企业接到生产一批设备的订单，要求不超过12天完成．这种设备的出厂价为1200元 台，该企业第一天生产22台设备，第二天开始，每天比前一天多生产2台．若干天后，每台设备的生产成本将会增加，设第 天 为整数）的生产成本为 （元 台）， 与 的关系如图所示．
（1）若第 天可以生产这种设备 台，则 与 的函数关系式为 ， 的取值范围为 ；
（2）第几天时，该企业当天的销售利润最大？最大利润为多少？
（3）求当天销售利润低于10800元的天数．
相关试题
直线y=x+m和抛物线y=x2+bx+c都经过点A（1，0），B（3，2）．
（1）求m的值和抛物线的解析式；
（2）求不等式x2+bx+c＞x+m的解集．（直接写出答案）
如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．
（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）当t为何值时，△CPQ为等腰三角形？
如图，在菱形ABCD中，AB＝4，∠BAD＝120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．
（1）证明：BE＝CF；
（2）当点E、F在BC、CD上滑动时，四边形AECF面积是否发生变化？如果不变，求出这个定值；
（3）设BE＝x，△CEF的面积为y，求y与x之间的函数关系式（不写出自变量x取值范围）．
中，直线
与
轴，
轴分别交于
两点，以
为边在第二象限内作矩形
，使
．
，点
的坐标；
作
轴，垂足为
，求证：
；推荐套卷
粤公网安备 44130202000953号