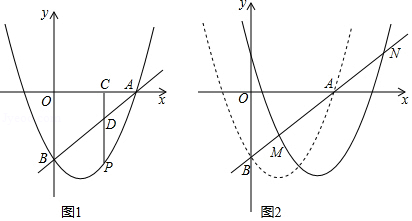
如图,抛物线 与 轴正半轴交于点 ,与 轴交于点 .
(1)求直线 的解析式及抛物线顶点坐标;
(2)如图1,点 为第四象限且在对称轴右侧抛物线上一动点,过点 作 轴,垂足为 , 交 于点 ,求 的最大值,并求出此时点 的坐标;
(3)如图2,将抛物线 向右平移得到抛物线 ,直线 与抛物线 交于 , 两点,若点 是线段 的中点,求抛物线 的解析式.
推荐套卷
如图,抛物线 与 轴正半轴交于点 ,与 轴交于点 .
(1)求直线 的解析式及抛物线顶点坐标;
(2)如图1,点 为第四象限且在对称轴右侧抛物线上一动点,过点 作 轴,垂足为 , 交 于点 ,求 的最大值,并求出此时点 的坐标;
(3)如图2,将抛物线 向右平移得到抛物线 ,直线 与抛物线 交于 , 两点,若点 是线段 的中点,求抛物线 的解析式.
