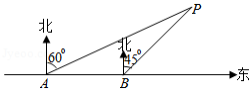
为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理.如图所示,正在执行巡航任务的海监船以每小时40海里的速度向正东方向航行,在处测得灯塔在北偏东方向上,继续航行30分钟后到达处,此时测得灯塔在北偏东方向上.
(1)求的度数;
(2)已知在灯塔的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?(参考数据:,
相关知识点
推荐套卷
为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理.如图所示,正在执行巡航任务的海监船以每小时40海里的速度向正东方向航行,在处测得灯塔在北偏东方向上,继续航行30分钟后到达处,此时测得灯塔在北偏东方向上.
(1)求的度数;
(2)已知在灯塔的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?(参考数据:,
