在画二次函数的图象时,甲写错了一次项的系数,列表如下
0 |
1 |
2 |
3 |
||||
6 |
3 |
2 |
3 |
6 |
乙写错了常数项,列表如下:
0 |
1 |
2 |
3 |
||||
2 |
7 |
14 |
通过上述信息,解决以下问题:
(1)求原二次函数的表达式;
(2)对于二次函数,当 时,的值随的值增大而增大;
(3)若关于的方程有两个不相等的实数根,求的取值范围.
相关知识点
推荐套卷
 ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).
ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).
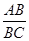 的值.
的值.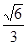 时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).
时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).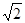 ≈1.414;
≈1.414;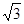 ≈1.732;
≈1.732;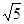 ≈2.236)
≈2.236)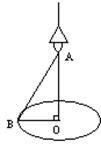
 ×100%)
×100%)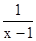 )÷
)÷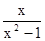 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号