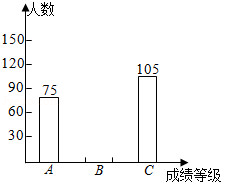
某校开展了“我爱古诗词”知识竞赛活动，将某年级参赛学生的成绩划分为三个等级进行统计分析，绘制得到如图表．
成绩等级 |
频数 |
频率 |
75 |
||
0.4 |
||
105 |
0.35 |
请结合图表信息，解答下列问题：
（1）该年级学生共有多少人？
（2）求表中，的值，并补全条形统计图；
（3）学校决定从参赛的甲、乙、丙、丁四名同学中任意抽取两名同学做经验介绍，求恰好选中甲、乙两位同学的概率．
如图①，P为△ABC内一点，连接PA，PB，PC，在△PAB，△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．
已知△ABC中，∠A＜∠B＜∠C
（1）利用直尺和圆规，在图②中作出△ABC的自相似点P（不写作法，但需保留作图痕迹）；
（2）若△ABC的三内角平分线的交点P是该三角形的自相似点，求该三角形三个内角的度数．
某校九年级学生共600人，为了解这个年级学生的体能，从中随机抽取部分学生进行1分钟的跳绳测试，并指定甲，乙，丙，丁四名同学对这次测试结果的数据作出整理，下图是这四名同学提供的部分信息：
甲：将全体测试数据分成6组绘成直方图（如图）.
乙：跳绳次数不少于105次的同学占96％.
丙：第①，②两组频率之和为0.12，且第②组与第⑥组频数都是12.
丁：第②，③，④组的频数之比为4:17:15．
根据这四名同学提供的材料，请解答如下问题：
（1）这次跳绳测试共抽取多少名学生？
（2）如果跳绳次数不少于135次为优秀，根据这次抽查的结果，估计全年级达到跳绳优秀的人数为多少？
已知：如图1，平面直角坐标系
中，四边形OABC是矩形，点A，C的坐
标分别为（6，0），（0，2）．点D是线段BC上的一个动点（点D与点B，C不重合），过点D作直线
＝－
＋
交折线O－A－B于点E．
（1）在点D运动的过程中，若△ODE的面积为S，求S与的函数关系式，并写出自变量的取值范围；
（2）如图2，当点E在线段OA上时，矩形OABC关于直线DE对称的图形为矩形O′A′B′C′，C′B′分别交CB，OA于点D，M，O′A′分别交CB，OA于点N，E．求证：四边形DMEN是菱形；
（3）问题（2）中的四边形DMEN中，ME的长为____________．
粤公网安备 44130202000953号