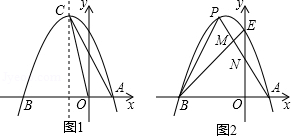
如图1,已知抛物线过点,.
(1)求抛物线的解析式及其顶点的坐标;
(2)设点是轴上一点,当时,求点的坐标;
(3)如图2.抛物线与轴交于点,点是该抛物线上位于第二象限的点,线段交于点,交轴于点,和的面积分别为、,求的最大值.
推荐套卷
如图1,已知抛物线过点,.
(1)求抛物线的解析式及其顶点的坐标;
(2)设点是轴上一点,当时,求点的坐标;
(3)如图2.抛物线与轴交于点,点是该抛物线上位于第二象限的点,线段交于点,交轴于点,和的面积分别为、,求的最大值.
