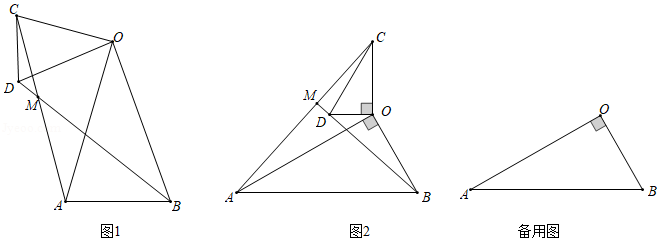
(1)问题发现
如图1,在和中,,,,连接,交于点.填空:
①的值为 ;
②的度数为 .
(2)类比探究
如图2,在和中,,,连接交的延长线于点.请判断的值及的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将绕点在平面内旋转,,所在直线交于点,若,,请直接写出当点与点重合时的长.
相关知识点
推荐套卷
(1)问题发现
如图1,在和中,,,,连接,交于点.填空:
①的值为 ;
②的度数为 .
(2)类比探究
如图2,在和中,,,连接交的延长线于点.请判断的值及的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将绕点在平面内旋转,,所在直线交于点,若,,请直接写出当点与点重合时的长.
