选修4-1：几何证明选讲
如图，过圆O外一点M作它的一条切线，切点为A，过A作直线AP⊥OM于P．
（1）证明：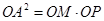
；
（2）N为线段AP上一点，直线NB⊥ON且交圆O于B点，过B点的切线交直线ON于K．证明：∠OKM=90°．
是定义在
上的奇函数，且
.
且
．
的值；
在
上的单调性，并给予证明．
，
．
；
，求实数
的取值范围．
－1，
}，B＝{
；
.
在[0，＋∞)上是减函数，试比较
与
的大小．推荐套卷
选修4-1：几何证明选讲
如图，过圆O外一点M作它的一条切线，切点为A，过A作直线AP⊥OM于P．
（1）证明：；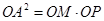
（2）N为线段AP上一点，直线NB⊥ON且交圆O于B点，过B点的切线交直线ON于K．证明：∠OKM=90°．
粤公网安备 44130202000953号