某电信检修小组从A地出发,在东西向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下。(单位:km)
| 第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
第七次 |
| -3 |
+7 |
-9 |
+8 |
+6 |
-5 |
-4 |
(1)求收工时距A地多远?
(2)在第几次纪录时距A地最远?
(3)若每km耗油0.2升,问共耗油多少升?
相关知识点
推荐套卷

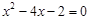
 ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.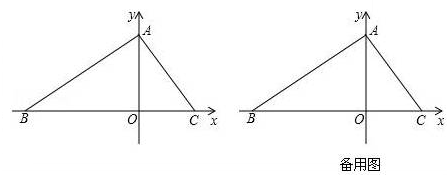
 粤公网安备 44130202000953号
粤公网安备 44130202000953号