在一副三角板ABC和DEF中,
(1)当AB∥CD,如图①。求∠DCB的度数。
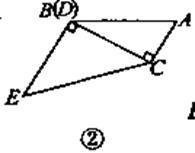
(2)当CD与CB重合时,如图②,判定DE与AC的位置关系,并说明理由。
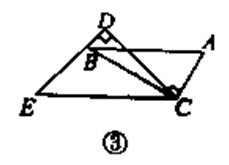
(3)如图③,当∠DCB等于多少度时,AB∥EC?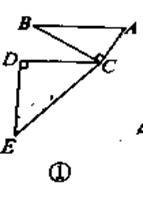
相关知识点
推荐套卷
在一副三角板ABC和DEF中,
(1)当AB∥CD,如图①。求∠DCB的度数。
(2)当CD与CB重合时,如图②,判定DE与AC的位置关系,并说明理由。
(3)如图③,当∠DCB等于多少度时,AB∥EC?

