在平面直角坐标系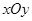 中,圆
中,圆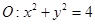 交
交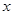 轴于点
轴于点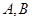 (点
(点 在
在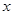 轴的负半轴上),点
轴的负半轴上),点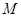 为圆
为圆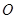 上一动点,
上一动点,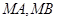 分别交直线
分别交直线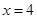 于
于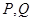 两点.
两点.
(1)求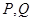 两点纵坐标的乘积;
两点纵坐标的乘积;
(2)若点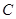 的坐标为
的坐标为 ,连接
,连接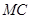 交圆
交圆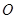 于另一点
于另一点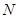 ,
,
①试判断点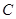 与以
与以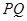 为直径的圆的位置关系,并说明理由;
为直径的圆的位置关系,并说明理由;
②记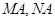 的斜率分别为
的斜率分别为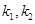 ,试探究
,试探究 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
相关知识点
推荐套卷
在平面直角坐标系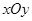 中,圆
中,圆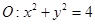 交
交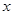 轴于点
轴于点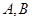 (点
(点 在
在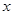 轴的负半轴上),点
轴的负半轴上),点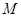 为圆
为圆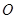 上一动点,
上一动点,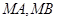 分别交直线
分别交直线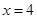 于
于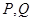 两点.
两点.
(1)求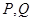 两点纵坐标的乘积;
两点纵坐标的乘积;
(2)若点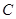 的坐标为
的坐标为 ,连接
,连接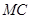 交圆
交圆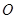 于另一点
于另一点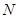 ,
,
①试判断点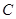 与以
与以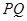 为直径的圆的位置关系,并说明理由;
为直径的圆的位置关系,并说明理由;
②记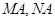 的斜率分别为
的斜率分别为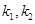 ,试探究
,试探究 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.