(本小题满分12分)
医生的专业能力参数K可有效衡量医生的综合能力,K越大,综合能力越强,并规定:能力参数K不少于30称为合格,不少于50称为优秀,某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力参数K的频率颁布直方图:
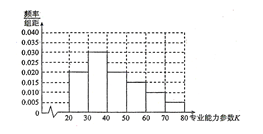
(1)求这个样本的合格率、优秀率,并估计能力参数K的平均值;
(2)现用分层抽样的方法从中抽出一个样本容量为20的样本,再从这20名医生中随机选出2名。
①求这2名医生的能力参数K为同一组的概率;
②设这2名医生中能力参数K为优秀的的人数为X,求随机变量X的分布列和期望。