如图，在Rt△ABC中，∠C=90°，∠A=30°．请把Rt△ABC分割成三个三角形，其中有两个三角形和原Rt△ABC相似，第三个三角形为等腰三角形．画图要求：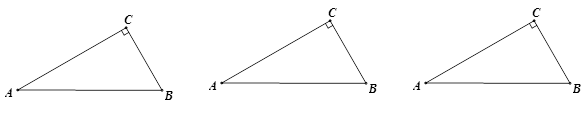
（1）工具不限，画图准确，标出能说明画法的符号或角度．
（2）用三种不同的方法画图，有一条分割线的位置不同即视为不同的画法．
相关试题
如图所示，在△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P从点A出发沿边AC向点C以1cm/s的速度移动，点Q从C点出发沿CB边向点B以2cm/s的速度移动．
（1）如果P、Q同时出发，几秒钟后，可使△PCQ的面积为8cm
？
（2）若点P从点A出发沿边AC-CB向点B以1cm/s的速度移动，点Q从C点出发沿CB-BA边向点A以2cm/s的速度移动。当点P在CB边上，点Q在BA边上，是否存在某一时刻，使得△PBQ的面积14.4 cm？
如图，每个小方格都是边长为1个单位的小正方形，B，C，D三点都是格点（每个小方格的顶点叫格点）．
（1）找出格点A，连接AB、AD，使得四边形ABCD为菱形；
（2）画出菱形ABCD绕点A逆时针旋转90°后的菱形AB1C1D1，并求点C旋转到点C1所经过的路线长．（结果保留
）
在
的直径
的延长线上，点
在
，
，
市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如表（单位：环）：
| 第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
第6次 |
|
| 甲 |
10 |
9 |
8 |
8 |
10 |
9 |
| 乙 |
10 |
10 |
8 |
10 |
7 |
9 |
（1）根据表中的数据，分别计算甲、乙两人的平均成绩：
=，
=
（2）分别计算甲、乙六次测试成绩的方差；S2甲= S2乙=
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由．
相关知识点
推荐套卷
粤公网安备 44130202000953号