如图,在平面直角坐标系中,直线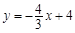 分别交x轴、y轴于A、B两点.
分别交x轴、y轴于A、B两点.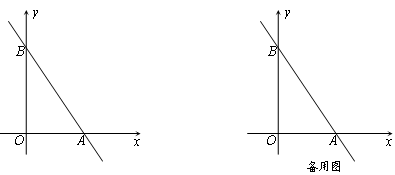
(1)求A、B两点的坐标;
(2)设P是直线AB上一动点(点P与点A不重合),⊙P始终和x轴相切,和直线AB相交于C、D两点(点C的横坐标小于点D的横坐标).若P点的横坐标为m,试用含有m的代数式表示点C的横坐标;
(3)在(2)的条件下,若点C在线段AB上,当△BOC为等腰三角形时求m的值.
相关知识点
推荐套卷
如图,在平面直角坐标系中,直线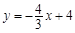 分别交x轴、y轴于A、B两点.
分别交x轴、y轴于A、B两点.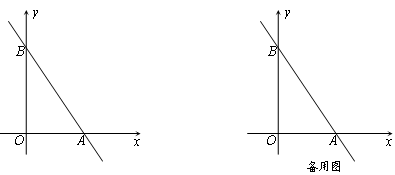
(1)求A、B两点的坐标;
(2)设P是直线AB上一动点(点P与点A不重合),⊙P始终和x轴相切,和直线AB相交于C、D两点(点C的横坐标小于点D的横坐标).若P点的横坐标为m,试用含有m的代数式表示点C的横坐标;
(3)在(2)的条件下,若点C在线段AB上,当△BOC为等腰三角形时求m的值.