如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形.除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为 ,其中
,其中 (
( ),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为
),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为 .
.
(1)当k=4时,若要求 为2的倍数,则有多少种不同的标注方法?
为2的倍数,则有多少种不同的标注方法?
(2)当k=11时,若要求 为3的倍数,则有多少种不同的标注方法?
为3的倍数,则有多少种不同的标注方法?
推荐套卷

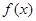 在区间
在区间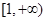 上的单调性
上的单调性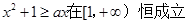 ,求参数
,求参数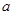 的取值范围。
的取值范围。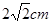 ,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式。
,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式。 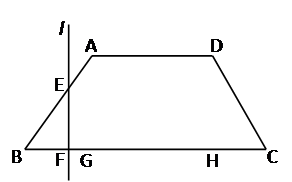
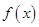 满足
满足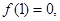 ,且
,且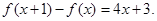
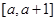 上单调,求实数
上单调,求实数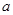 的取值范围.
的取值范围.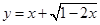 的值域
的值域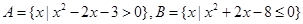 ,
,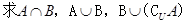
 粤公网安备 44130202000953号
粤公网安备 44130202000953号