已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
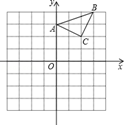
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
相关知识点
推荐套卷

 ≥2(4)-1≤x<2
≥2(4)-1≤x<2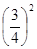 2×1×
2×1×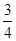 ;
;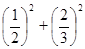
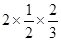 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号