这是某单位的平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1).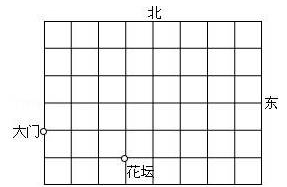
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出A点的位置.
(3)建筑物B在大门北偏东45°的方向,并且B在花坛的正北方向处,请直接写出B点的坐标.
(4)在y轴上找一点C,使△ABC是以AB腰的等腰三角形,请直接写出点C的坐标.
相关知识点
推荐套卷
这是某单位的平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1).
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出A点的位置.
(3)建筑物B在大门北偏东45°的方向,并且B在花坛的正北方向处,请直接写出B点的坐标.
(4)在y轴上找一点C,使△ABC是以AB腰的等腰三角形,请直接写出点C的坐标.