如图，有一个长为24米的篱笆，一面利用墙（墙的最大长度a为15米）围成的中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S平方米．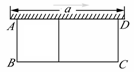
（1）求S与x的函数关系式；
（2）如果要围成花圃的面积为36平方米，求AB的长为多少米？
（3）如果要使围成花圃面积最大，求AB的长为多少米？
相关试题
如图，有一个长为24米的篱笆，一面利用墙（墙的最大长度a为15米）围成的中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S平方米．
（1）求S与x的函数关系式；
（2）如果要围成花圃的面积为36平方米，求AB的长为多少米？
（3）如果要使围成花圃面积最大，求AB的长为多少米？
、
、
轴的对称图形
，写出
的坐标。
，它的最长边是8cm，求它的最短边的长。
处王老师交帐说：“我买了两种书，共105本，单价分别为8元和12元，买书前我领了1500元，现在还余418元.”王老师算了一下，说：“你肯定搞错了.”
粤公网安备 44130202000953号