如图,在四棱柱 中,侧棱
中,侧棱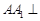 底面
底面 ,
,

(Ⅰ)求证: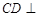 平面
平面 ;
;
(Ⅱ)若直线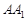 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值.
(Ⅲ)现将与四棱柱 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为 ,写出
,写出 的解析式.(直接写出答案,不必说明理由)
的解析式.(直接写出答案,不必说明理由)
推荐套卷
如图,在四棱柱 中,侧棱
中,侧棱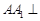 底面
底面 ,
,

(Ⅰ)求证: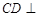 平面
平面 ;
;
(Ⅱ)若直线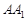 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值.
(Ⅲ)现将与四棱柱 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为 ,写出
,写出 的解析式.(直接写出答案,不必说明理由)
的解析式.(直接写出答案,不必说明理由)