甲乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛，若赛完5局仍未出现连胜，则判定获胜局数多者赢得比赛，假设每局甲获胜的概率为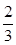
，乙获胜的概率为
，各局比赛结果相互独立．
（1）求甲在4局以内（含4局）赢得比赛的概率；
（2）记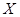
为比赛决出胜负时的总局数，求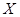的分布列和均值（数学期望）．
相关试题
，求实数
的取值范围．
，且
，函数
．
的解析式；
．
的定义域；（2）判断
上的单调性．
且对任意实数
求
在（Ⅰ）的条件下，当
是单调函数，求实数
的取值范围．
＋ln
＋
；
，求
．推荐套卷
甲乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛，若赛完5局仍未出现连胜，则判定获胜局数多者赢得比赛，假设每局甲获胜的概率为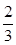，乙获胜的概率为，各局比赛结果相互独立．
（1）求甲在4局以内（含4局）赢得比赛的概率；
（2）记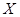为比赛决出胜负时的总局数，求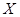的分布列和均值（数学期望）．
粤公网安备 44130202000953号