计算化简或解方程:
(1)(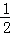 ﹣
﹣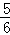 ﹣
﹣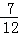 )×(﹣36)
)×(﹣36)
(2)(﹣1)3×(﹣5)÷[﹣32+(﹣2)2]
(3)5x+y﹣3(x﹣3y)
(4)3x﹣2(10﹣x)=5
(5) ﹣
﹣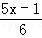 =1;
=1;
(6)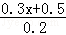 ﹣
﹣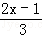 =1.
=1.
相关知识点
推荐套卷
计算化简或解方程:
(1)(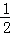 ﹣
﹣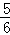 ﹣
﹣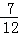 )×(﹣36)
)×(﹣36)
(2)(﹣1)3×(﹣5)÷[﹣32+(﹣2)2]
(3)5x+y﹣3(x﹣3y)
(4)3x﹣2(10﹣x)=5
(5) ﹣
﹣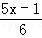 =1;
=1;
(6)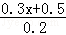 ﹣
﹣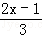 =1.
=1.