星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(立方米)与时间x(小时)的函数关系如图所示.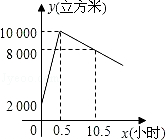
(1)8:00~8:30,燃气公司向储气罐注入了多少立方米的天然气;
(2)当x≥0.5时,求储气罐中的储气量y(立方米)与时间x(小时)的函数解析式;
(3)请你判断,正在排队等候的第18辆车能否在当天10:30之前加完气?请说明理由.
相关知识点
推荐套卷
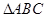 中,BE、CF分别平分
中,BE、CF分别平分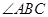 和
和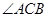 ,
,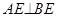 于E,
于E, 于F,求证:EF//BC
于F,求证:EF//BC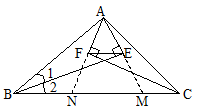

 粤公网安备 44130202000953号
粤公网安备 44130202000953号